当NPOでは電柱無くすことによる様々な恩恵を調査してきました。その中で電柱を無くすのメリットの一つとして「電柱を無くせば、景観が良くなる」というもののが存在します。直感的に空を覆う電線が無くなれば眺めが良くなることはなんとなく理解できると思います。

果たしてこの景観は良いのか悪いのか? 引用元:http://mudenchuka.jp/
しかしながら、景観は見る人によって受け取り方が違い、曖昧なものです。人によっては、電柱が目立つ街並みに魅力を感じる方もいらっしゃると思います。そこで電柱が景観に与える影響を調べることによって、電柱がプラスの効果を持つのか、マイナスの効果を持つのかを検証したいと思います。そうすることによって、電柱の社会的立場を明らかにすることができます。
そもそも良い景観とはなんだろうか?
そもそもいい景観とはどういったものを指すのでしょうか。平成23年に国土交通省が行った「景観に関する意識調査」では、次のような結果となっています。
Q.あなたが思う優れた景観とはどのようなものですか。二つまでご回答ください。
| 割合 | |
| 1.閑静な住宅地・のどかな集落の景観 | 34.5% |
| 2.駅前等の賑わいある景観 | 11.9% |
| 3.穏やかな田園景観 | 24.1% |
| 4.河川た海岸線等の水辺のうるおいある景観 | 37.0% |
| 5.緑地や樹林地等の緑の景観 | 52.7% |
| 6.歴史的な景観 | 37.5% |
| 7.その他 | 6.0% |
| 無回答 | 0.1% |
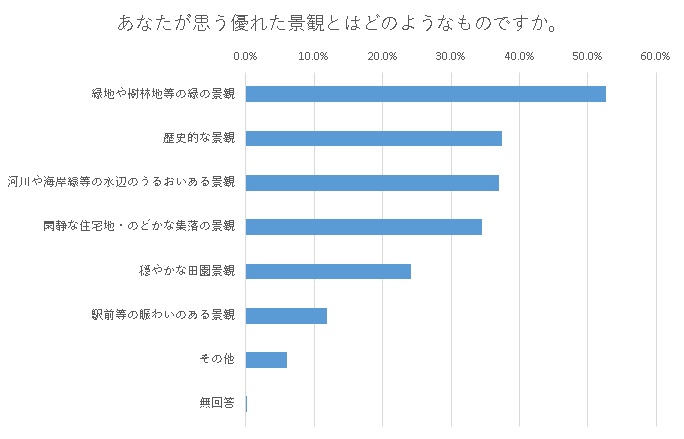
この結果から駅前等の賑わいのある景観はあまり支持されておらず、緑を中心とした景観が一般的に好まれているようです。

巣鴨地蔵通り商店街

根津神社
このアンケートの結果から「良い景観」と感じるためには「景観が複雑ではない」ということを条件にしていると考えられます。当然、これに関しては様々な意見があると思います。
しかしながらここでは電柱の社会的立場を明らかにしようという試みなので、多数派の意見を採用したいと思います。またこれに関しての考察は後述します。
なぜ良い景観を目指すのか
「良い景観」とはなにかという問題と併せて、「なぜ良い景観を作らなければならないか」という問題も存在するでしょう。
先ほども触れましたが、人それぞれ「良い景観」というものは違うはずです。それでも「景観政策」と呼ばれる緑化や無電柱化等、多額の税金を使ってまで事業を進めようとするのでしょうか。

イギリス、ノースヨークシャー郡にあるハロゲイト町。地方都市でも整然とした街並みを形成している。
これに関して、「良い景観」には精神的な面と経済的な面にメリットがあるようです。
景観法の第1条の中で「美しく風格のある国土の形成、潤いのある豊かな生活環境の創造及び個性的で活力ある地域社会の実現を図り、もって国民生活の向上並びに国民経済及び地域社会の健全な発展に寄与することを目的とする」とされている通り、「良い景観」には国民生活の向上効果があることが法律として明記されています。
他にも経済的な面を詳しく検証した資料として財団法人都市づくりパブリックデザインセンター発行の「景観形成の経済的価値分析に関する検討報告書」がありますので興味のある方は参考にしてみて下さい。
客観的に「良い景観」かどうかを判断する方法
さてここからが本題です。「電柱が景観にどのような影響を与えているのか」という問題に、従来はアンケートを用いて調査されてきました。当然アンケートですからこの問題に対する「性質」を調べるのに役立ちますが、「数字」として具体的に表すことができませんでした。
しかしこの問題を「数字」という視点から分析しようとする画期的な試みがありました。石田他が発表した「無電柱化整備による道路のシークエンス景観の効果計測に関する研究」(2011)をもとに簡単に説明していきます。

コンピューターが「良い景観」かどうかを判定する
まず、電柱がある道路の写真を撮影します。次に撮った写真を画像加工して電柱と電線のみを消去した画像を作ります。ここで、「電柱が映り込んでいる写真」と「画像加工によって電柱が消去された画像」を「画像の複雑さ(※1)」という尺度でコンピューターによって数値化し、どちらがより複雑かという判定を行うというものです。
「画像の複雑さ」は1から2までの間の小数で判定されて、1に近い場合は単純な景観(=前述した「良い景観」)で2に近い場合は複雑な景観となります。
これらをまとめると、「電柱がある道路の画像」と「加工によって電柱を除去した道路の画像」とをコンピューターを使って解析して、「画像の複雑さ」がどう変化したかを比較するのが今回の調査方法です。

各地点の代表点例…引用:石田他「無電柱化整備による道路のシークエンス景観の効果計測に関する研究」(2011)
(※1)・・・ここでいう「画像の複雑さ」をフラクタル次元という。フラクタル次元は次元の値が整数にならない次元の概念であるが、詳しくは補足を参考にしていただきたい。
調査結果
先述した方法で画像を比較してみると次のような結果が分かりました。
各画像の「画像の複雑さ」の数値
| カテゴリ | 整備前 | 整備後 | 低下量 |
| 商業地域A | 1.83 | 1.82 | 0.01 |
| 商業地域B | 1.82 | 1.81 | 0.01 |
| 商業地域C | 1.83 | 1.81 | 0.02 |
| 近隣商業地域A | 1.80 | 1.77 | 0.03 |
| 近隣商業地域B | 1.83 | 1.79 | 0.04 |
| 近隣商業地域C | 1.80 | 1.77 | 0.03 |
| 住宅地域A | 1.76 | 1.74 | 0.02 |
| 住宅地域B | 1.75 | 1.71 | 0.04 |
| 住宅地域C | 1.79 | 1.70 | 0.09 |
| 地方部中心街A | 1.84 | 1.81 | 0.03 |
| 地方部中心街B | 1.77 | 1.73 | 0.04 |
| 地方部中心街C | 1.82 | 1.78 | 0.04 |
| 観光ルートA | 1.70 | 1.62 | 0.08 |
| 観光ルートB | 1.81 | 1.80 | 0.01 |
| 観光ルートC | 1.74 | 1.70 | 0.04 |
先ほども述べたように「画像の複雑さ」は1から2までの小数値で、2に近いほど画像が複雑になっていることを示しています。したがってこれらの数値の結果からすべての画像について電柱を除去することによって、「画像の複雑さ」が下がったということが分かりました。言い換えると、電柱を無くせば景観が単純になることを示唆しています。単純さが「良い景観」の条件とするならば、電柱を無くすことによって景観は良い方向に向かうと言ってもよいでしょう。
「画像の複雑さ」という数字と人間の感情との関係
先ほどまで言っていた「画像の複雑さ」はあくまでコンピューターが計算を行った結果です。人間が実際に画像をみて「これは良い景観になった」と思わなければ「画像の複雑さ」と「人間の感情」との間に関係がなくなってしまいます。また、国交省のアンケートによって半ば強引に決めた「良い景観の条件は単純さ」という仮定が間違っていないかどうかの確認にもなります。
機械が判定した「画像の複雑さ」と人間が「良い景観」と思うかどうかということの間に関係があるのだろうか?
ここで電柱があるとないとで人間に与える心理的効果を明らかにするためにアンケートを行います。各15地点の無電柱化が景観の変化に与える印象について次の6つの要素についてどう変わったかを問いました。
まず景観要素として①景観の変化、②構造の美、③色彩の美、そして空間要素として①広々感、②安全性、③雰囲気です。
これらのアンケートの要素を「総合要素」としてまとめ、「総合要素」の得点(※1)と「画像の複雑さ」の低下量を比較してみるとその妥当性が分かるはずです。つまり総合要素が高ければ低下量も高く、逆も然りといった具合であれば「画像の複雑さ」と人間の感情との間に関係が存在するはずです。
| 順位 | 道路景観画像 | 総合要素 | 「画像の複雑さ」低下量 |
| 1 | 住宅地域C | 3.472 | 0.0875 |
| 2 | 観光ルートA | 2.875 | 0.0818 |
| 3 | 住宅地域B | 1.218 | 0.0434 |
| 4 | 観光ルートC | 0.844 | 0.0351 |
| 5 | 観光ルートB | 0.770 | 0.0105 |
| 6 | 住宅地域A | 0.747 | 0.0216 |
| 7 | 近隣商業地域A | 0.578 | 0.0299 |
| 8 | 地方中心街A | -0.401 | 0.0274 |
| 9 | 商業地域C | -0.520 | 0.0169 |
| 10 | 地方中心街B | -0.786 | 0.0414 |
| 11 | 商業地域A | -1.011 | 0.0055 |
| 12 | 近隣商業地域B | -1.479 | 0.0354 |
| 13 | 地方中心街C | -1.509 | 0.0359 |
| 14 | 商業地域B | -1.771 | 0.0109 |
| 15 | 近隣商業地域C | -3.028 | 0.0347 |
表に示したランキングによると「総合要素」が上位の地点(住宅地域・観光ルート)は画像自体の青空が占める割合が大きい為電線や、電柱を無くすことによって広大な空が際立っています。つまり景観という観点において無電柱化をする効果が高いのはこれらの地域であることが分かります。
一方で、下位を占める「総合要素」が低い道路景観は、野外広告物や建物高さなどの規制が緩和されている地域であったと推察されます。これらの地域はまず景観規制を行って、「画像の複雑さ」を低下させることから始めなければならないでしょう
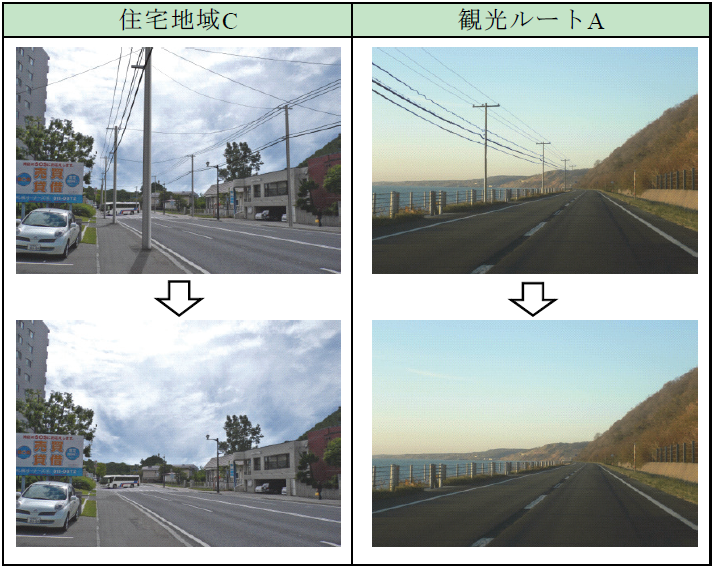
上位の画像はもともと写真に対する青空の割合が高い写真であった。
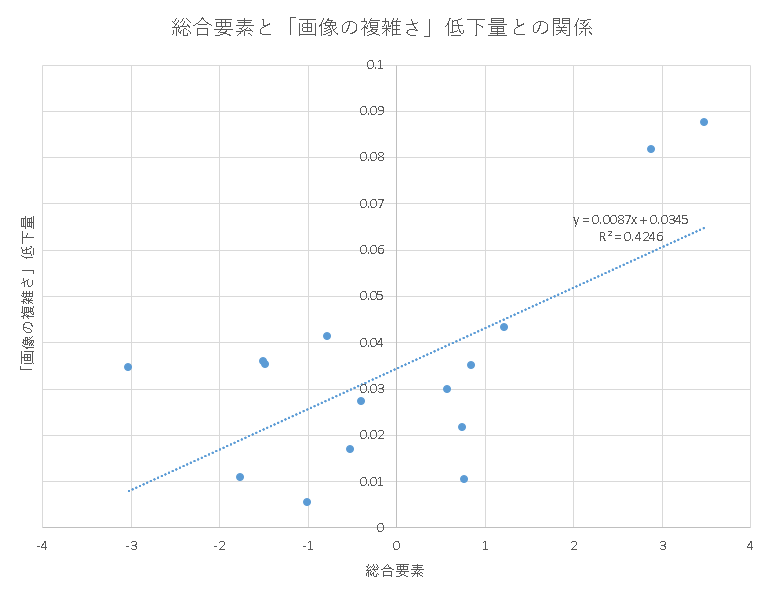
総合要素と「画像の複雑さ」低下量との関係。線形近似を行うと相関係数が0.425となり相関が存在するといえる。
(※1)・・・「総合要素」の得点化について、主成分分析を行って求めた主成分1が総合要素を表しているとして解釈している。
まとめ
「景観」というあやふやで価値基準がないものをどうやって評価するかを考えてきました。国土交通省の景観のアンケートより「良い景観」というものを「景観が複雑すぎないこと」と定めて電柱が景観に与える影響を調べることにしました。
この調査方法として「画像の複雑さ」というあまり聞きなじみのない言葉を用いて「電柱がある写真」と、「画像加工して電柱を消去した写真」とを比較しました。
すると、電柱がある写真と比べて電柱を消去した写真の方が「画像の複雑さ」が低下しました。
ここでアンケートを用いて、果たして本当に「画像の複雑さ」が低ければ人間が「良い景観」と思うかを調べました。
アンケートの結果、すべての質問項目をまとめた「総合要素」の得点と「画像の複雑さ」の低下量を比較すると、その二つには結びつきがあることがわかりました 。つまり最初に定めた「良い景観の条件は景観が複雑すぎないこと」という仮定が正しかったことを示しています。
長々と書いてきましたが、ここまでのことを一言でまとめると、「一般的に電柱は景観の邪魔になっている。」といういたってシンプルな結論が出てきました。しかしながら、従来から見られるこの手の主張には根拠がなく説得力が薄いものばかりでしたので、心強いエヴィデンスになるのではないでしょうか。
また当NPOでは防災に関する電柱の記事や電柱が地価に与える影響を調査した記事等ありますので、そちらをご覧になれば、電柱が社会に与える様々な影響について知ることができると思います。
参考文献
石田信二他:無電柱化整備による道路のシークエンス景観の効果計測に関する研究,土木学会論文集D1(景観・デザイン)Vol67,2011
お問い合わせ
補足:「画像の複雑さ」について
この記事の中に頻繁に出てくる「画像の複雑さ」という値に関する情報を少しだけ捕捉したいと思います。少し数学的な内容も含まれますので興味のある方だけお付き合いください。
先の米印でも書きましたが「画像の複雑さ」とはフラクタル次元の事です。定義に関して簡単に触れると、図形の各方向に1/lずつ縮めると元の図形を埋めるためにはN=lD個(ただしDはユークリッド次元)の自己相似図形が必要になります。この次元数Dを求めるためには対数を用いて計算します。しかしながら通常の次元で説明することのできない図形も存在します。例としてコッホ曲線はD=log4/log3≒1.26というフラクタル次元を持ちます。
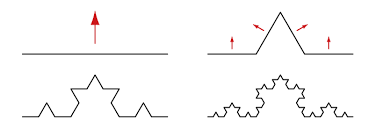
コッホ曲線
このコッホ曲線の弧長は操作を続けるうちに無限大へと近づいていきますが、平面とするには小さいことから1次元と2次元の間の数字をフラクタル次元として表しているのです、したがって前述したとおりフラクタル次元が1に近ければ近いほど図形は単純であり、2に近ければ複雑になるというわけです。
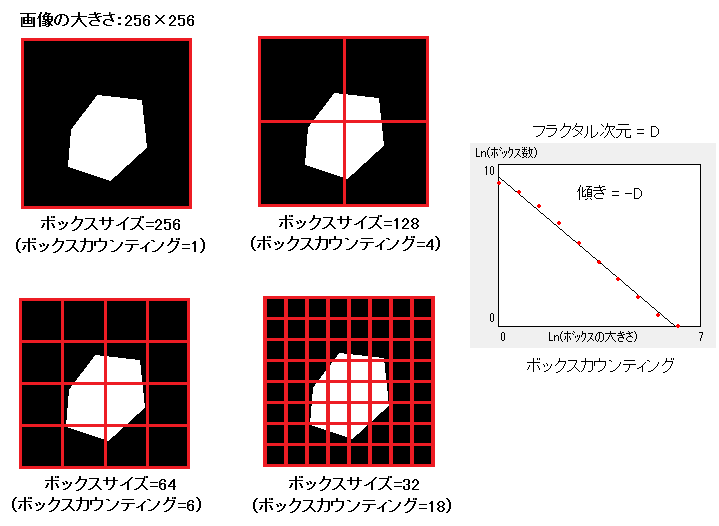
しかし実際の画像に純粋なフラクタル幾何の解析方法で計算することは困難であることは想像がつくと思います。そこでボックスカウント法と呼ばれる手法を用いて画像を解析します。解析手順は以下の通り
①図形を格子で覆う。
②図形の構成要素が存在する格子の数をカウントする。
③格子の大きさを変化させながら、同じように格子の数をカウントしていく。
④格子の大きさとカウントした格子の数を両対数グラフにプロットし最小自乗曲線を求める。
⑤乗数をフラクタル次元数とする。
最後に補足の補足となりますが、画像の線のみを抜き出さなければならないのでプレヴィット法と呼ばれるエッジを抽出する方法を用いてボックスカウント法を適用しているようです。
加工前 加工後 引用元:http://www.mis.med.akita-u.ac.jp/~kata/image/sobelprew.html